Absolute GPS to better than one meter - Page 2
2. General Formulas
To illustrate our data reduction procedures, we will present a sample calculation in section 4. This section describes the theory and formulas used.
Our reference frame will be the Earth-centered inertial (ECI) frame with origin at Earth’s center of mass. Let the Z axis point toward Earth’s north rotation pole. Then the X and Y axes will lie in the plane of the equator, with the X axis pointing toward the vernal equinox (the zero point for right ascension on the sky), and the Y axis 90° ahead in the direction of Earth’s rotation. Let a GPS satellite transmit a signal at a known time T according to its own clock, and let the satellite coordinates at that time be (X, Y, Z).
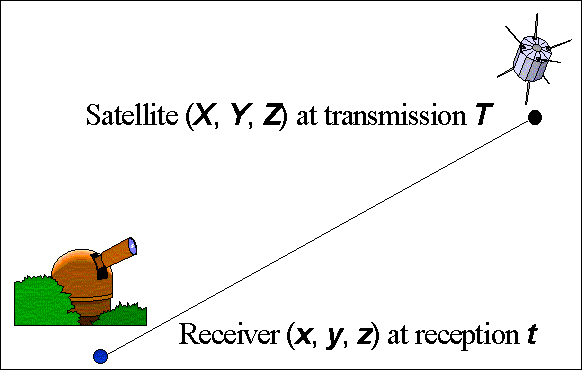
Figure 1. Schematic of pseudo-range, the observed quantity.
Roughly 80 milliseconds (ms) later, the signal traveling at the speed of light will be registered by a GPS receiver on the ground at timetaccording to the monitor station receiver’s own ground clock. Let the coordinates of the receiver in the ECI frame at reception timetbe (x,y,z). SeeFigure 1. If all these quantities are known in advance, then the distance traveled by the signal in the ECI frame between transmission and reception,r, is given by:
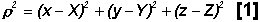
In normal field use, however, neither the satellite coordinates nor the receiver coordinates are known precisely in advance. Our problem differs somewhat from that for the standard GPS receiver in that we do know the receiver coordinates in advance to bout a meter, whereas usually they must be taken as unknowns. And normal GPS receivers do not have their own atomic clocks, but must infer the time along with their own coordinates from the satellite-provided information; whereas the Air Force monitor station receivers do have their own atomic clocks. But in principle, the problem is nearly the same, and all assumed coordinates ust be corrected with the help of the observational data.
So the quantity actually measured is the time interval (t - T) as judged entirely by the receiver clock. If both clocks were synchronized in the ECI frame and kept perfect time, then (ignoring propagation delays) r = c(t-T), where c is the speed of light. But in practice, both clocks have errors. The receiver cannot tell when the signal was actually transmitted, but knows only when the instant T occurred for its own clock. Because these clock errors can be appreciable (up to about 0.7 ms in 1993) and cannot be precisely known until an analysis has been performed, the observed quantity factored by c is called a "pseudo-range" (PR) instead of simply a range.
In addition to this signal transit delay, GPS receivers can also detect a carrier signal from the satellites and count cycles of the carrier wave to determine any changes in the distance of the source from the receiver. The phase of the wave enables interpolation between cycles to high precision. This interpolated cycle count, scaled appropriately to convert it to meters, is called the "accumulated delta range", or ADR. When the satellite is first acquired, the ADR is set to zero. Subsequently, the ADR is rigorously proportional to the change in signal delay since acquisition unless it accidentally misses one or more whole cycles in its count (called "cycle slips" – an infrequent occurrence that does occasionally happen). Ignoring cycle slips, the ADR should differ from PR only by a single constant for each pass of each satellite over each station. However, in practice, the ionosphere affects ADR differently than PR, so some additional modeling is needed for maximum accuracy. The advantage the ADR has over PR is that it can be measured far more precisely. The disadvantages are cycle slips and the additive constant. In what follows, remarks applicable to PR values also apply to ADR values unless otherwise specified.
We have essentially a continuous record of PR and ADR between each satellite-receiver pair while the satellite is above about 6° altitude. So it is not difficult to use the unique signatures of the various possible error sources to solve for corrections to the satellite orbital elements, the receiver coordinates, and the clock errors. One clock must have a known relation to the US Naval Observatory Master Clock; and for our purposes, we have taken the Colorado Springs monitor station clock as having exactly the error indicated by the NRL data. Then all other satellite and monitor station clock corrections are relative to the USNO Master Clock via the Colorado Springs clock.
The observed PR (and ADR) are as provided by the Air Force. The calculated ranges for comparison use the input values of all parameters. This allows us to form an observed minus calculated (O - C) range correction to be analyzed. If the errors of the satellite elements, station coordinates, and clocks were removed, the remaining (O - C)s (called the "residuals") should resemble Gaussian noise and represent the intrinsic errors in the observed PR. If, however, they are not Gaussian, but rather are highly systematic, this indicates additional predictable effects that need to be identified and applied as corrections. Several such effects have been identified and are discussed in the analysis section of this paper.
To form the (O - C)s, we need to specify the relation between the ECF and ECI coordinate systems. Then we need to apply corrections to the observed PR for clock errors and signal delays due to the Earth’s ionosphere and troposphere. Numerous other small corrections for the effects of relativity, solid-Earth tides, demodulator cable delays, the finite size of the satellites, etc., must also be applied. These corrections are discussed in detail in section 3. For the moment, we will consider a simple, classical, geometric analysis.
Let t be any MJD and fraction measured in days. Then GPS time as used in the GPS system, and Universal Time (e.g. UT1) as used in most astronomical applications, differ by an ever increasing number of seconds that can be approximated over our 4-day span of data as:
GPS-UT1 = 8.515 + 0.00216 (t- MJD 49,221.0) [2]
in seconds. The reference MJD epoch used here corresponds to 1993 Aug. 22.0, the beginning of the GPS week for which we have data. This formula is based on data supplied by the U.S. Naval Observatory Time Service. Because both our satellite and receiver coordinates are initially expressed in the ECF system, small errors in equation[2], or even neglecting this difference altogether, would affect both rotations to the ECI system equally, leaving us in an improperly oriented ECI system. Such errors would have negligible effect on our residuals or analysis. But since this correction can be included effortlessly, we do so.
Both the ECF and ECI frames have the same center and same z axis. They differ in that the x axis points toward the vernal equinox (a fixed direction in space) for the ECI frame, and toward the meridian of Greenwich for the ECF frame. Over the 15-minute time spans covered by the JPL satellite state vectors, precession, nutation, polar motion, and Earth rotation variations can all be neglected, and the assumption of uniform spin is quite adequate. So we use the standard IAU formula to convert Universal Time (UT1), expressed as a JD and fraction, to Greenwich Mean Sidereal Time (GMST), expressed as an angle, at any UT1 epochT, measured in Julian centuries from the standard epoch J2000. Therefore,T= (UT1 - JD 2,451,545.0) / 36525. Then:
GMST = 67 310.54841 + 3 164 4 00 184.812 866T+ 0.093 104T2- 0.000 006 2T3[3]
measured in seconds of time. Multiples of 86,400 seconds (one day) may be discarded, and the result multiplied by 2p / 86,400 to convert it to radians. A correction for the "equation of the equinoxes" is neglected because the PR and its analysis are unaffected by small rotations of the coordinate axes. If desired, this calculation is documented in (Seidelmann, 1992), or may be taken from the U.S. Naval Observatory NOVAS programs, available on the Web atwww.usno.navy.mil.
For computing geometric pseudo-ranges, it will be more convenient to use ECI coordinates because it is an inertial frame, and because it is easier to allow for the observer motion during the downlink time in that frame. So we will rotate the given ECF state vectors to the ECI frame. LetRn(q) be an operator that rotates a vectorV={Vx,Vy,Vz} through an angleqabout thenaxis, wheren= 1, 2, or 3 for axisx,y, orz, respectively. For example:
R3(q) {Vx,Vy,Vz}º{Vxcos(q) +Vysin(q), -Vxsin(q) +Vycos(q),Vz}[4]
for rotations about thezaxis. So if we setq= -GMST (in radians) in this formula, we will have the formula for the rotation from ECF to ECI coordinates that we seek.
Velocity vectors may be rotated from one frame to the other also. However, more than a direction change is involved. The angular velocity of rotation of the coordinate frame affects the magnitude of the satellite velocities in that frame as well. This angular velocity is such that objects fixed on the rotating Earth have zero velocity in the ECF frame. However, because satellites are typically about four Earth radii away, the angular velocity of the frame corresponds to roughly four times the linear velocity of the surface of the Earth at satellite distances. So when satellite state vectors are given in the ECF frame, even though the station velocities in that frame are zero, the satellite velocities arenotequal to the relative velocity between satellite and station. This trick of rotating reference frames, like the illusory coreolis forces that can magically appear, must be handled carefully to avoid computation errors for velocity-dependent quantities.
The transformation of velocities from ECF to ECI is therefore accomplished by first removing the effect of the rotation of the frame, then by rotating the remaining vector in the same way as for position usingR3(q). The first correction is accomplished usingq’= rate of change of GMST = 0.00007292115147 radians/second:
{x’,y’,z’}ECI= {x’-yq’,y’+xq’,z’}ECF[5]
For the calculation of expected pseudorange values, we must rotate the satellite state vector using GMSTt, the value of GMST at the time of satellite transmission. And we must rotate the receiver state vector using GMSTr, the value of GMST at the time of signal reception at the ground station. For highest accuracy, we should also consider the very small correction to GMST introduced by known clock errors, which can be of order of 0.7 ms in time.
Lettbe the Modified Julian Date of the nominal GPS observation time measured in days, andDtbe a clock correction in ns taken from Table 3:Dtsfor the satellite clock andDtmfor the monitor station clock. Then:
Dt= {PHASE} + 0.0864 {FREQ} (t- {MJD}).
We are given the nominal GPS observation timet, always an integral multiple of 1.5 seconds, as part of the observed pseudo-range. The actual GPS time of signal transmission is thent+Dts, the instant that the satellite thinks is timet. The actual GPS time of reception may be estimated with sufficient accuracy for purposes of computing GMST ast+Dts+r0/c, wherer0is a close guess ofrusing equation[1]with position coordinates in the ECF frame (e.g., those in Table 1 and Table 4) at the nominal GPS time of transmission, instead of positions in the ECI frame as they technically should be. Note that the GPS time of reception is independent of the error for the receiver clock, which affects only the observed PR and ADR values, but not their GPS epoch.
Finally, the value of Universal Time UT1 to be converted toTand used in equation[3]is found by subtracting {GPS-UT1} in equation[2]. So for transmission and reception events, respectively:
UT1t=t+Dts- {GPS-UT1} [6]
UT1r=t+Dts+r0/c- {GPS-UT1}
which then lead directly to GMSTtand GMSTrvia equation[3]. In practice, we will generally apply equation[3]only once using UT1 =t, then correct that computed GMST to other times as indicated in equation[6]using the fact that GMST changes at a very nearly uniform rate of 1.002 737 9 seconds per second = 0.000 072 921 15 radians per second. (Note: If we had been using standard GPS receiver data for an unknown station location instead of known monitor stations,r0would be unknown, and we would need to estimate the station coordinates usingr0= 0 (or some other estimate) first, and then iterate.)
